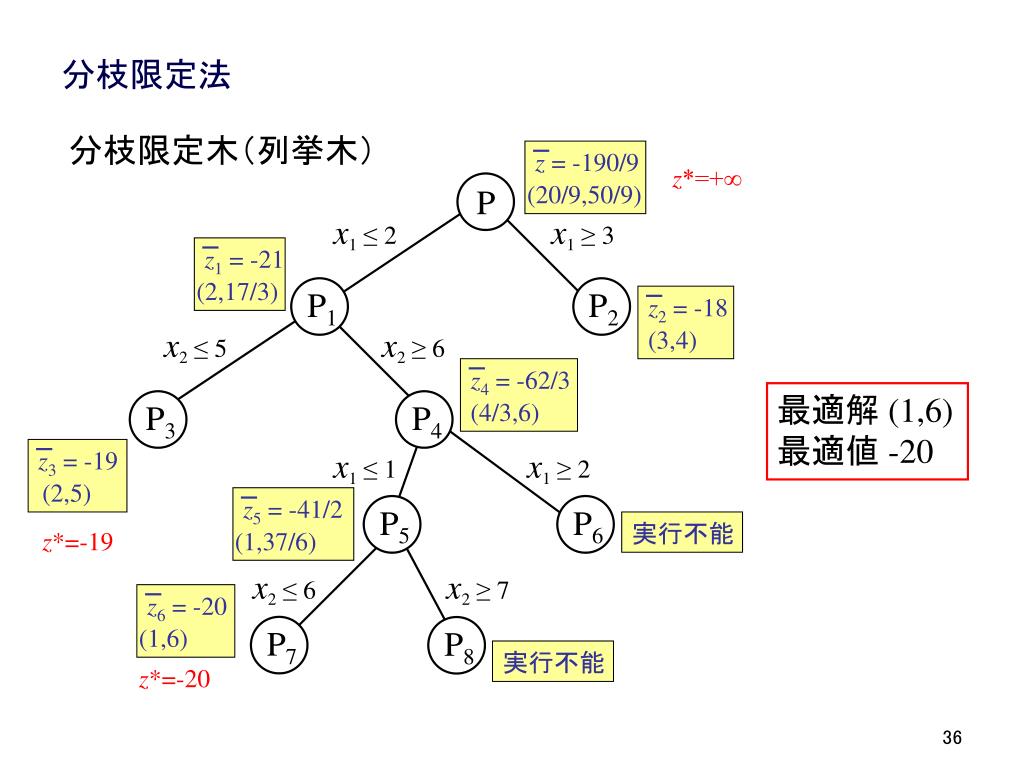
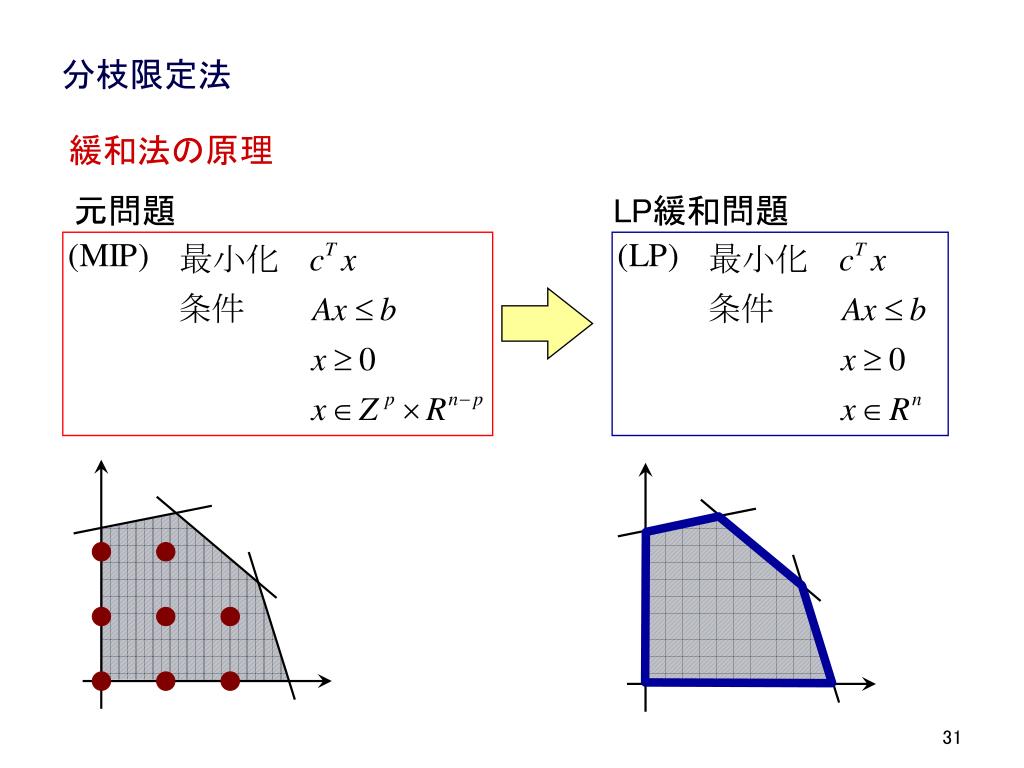
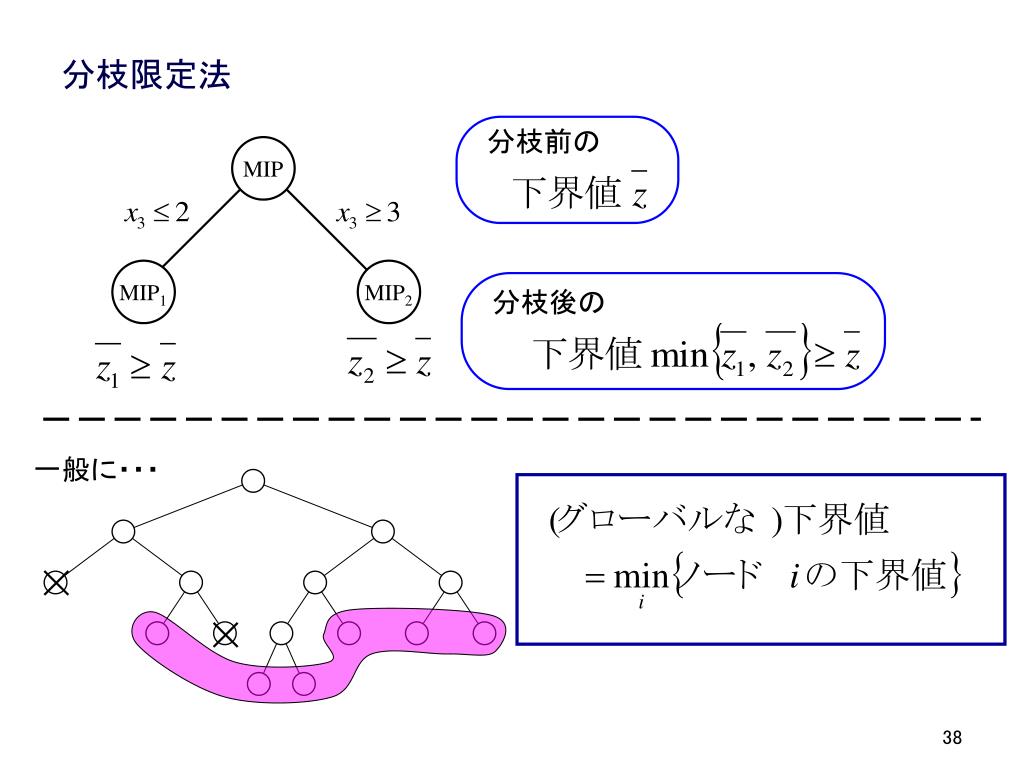
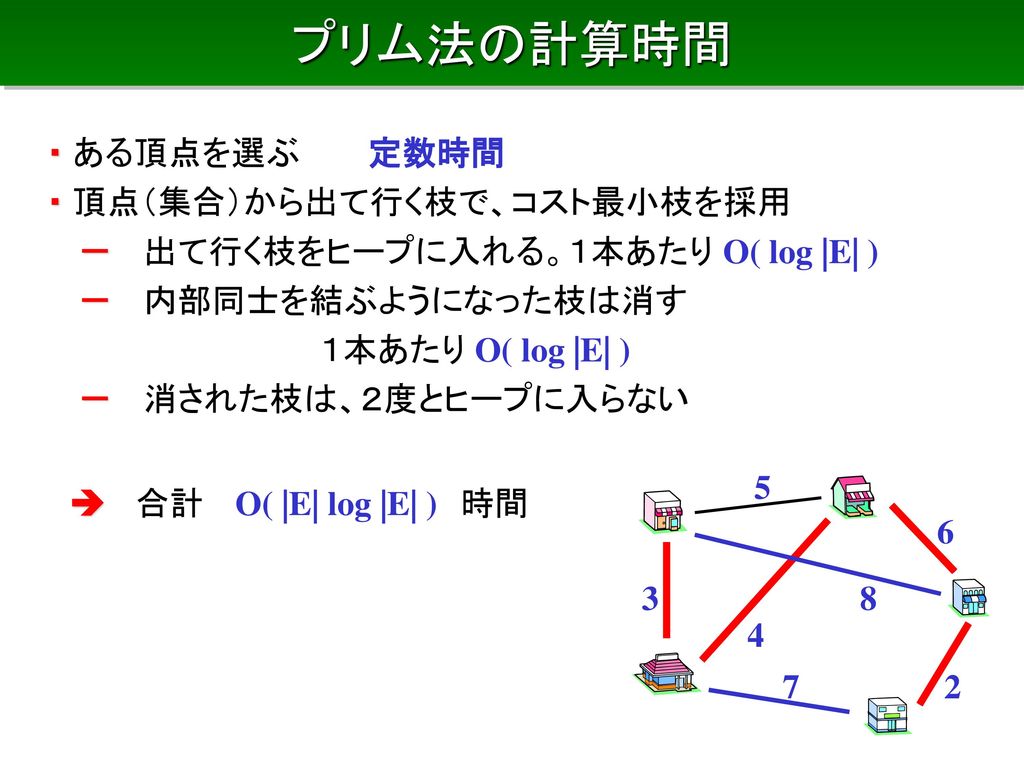
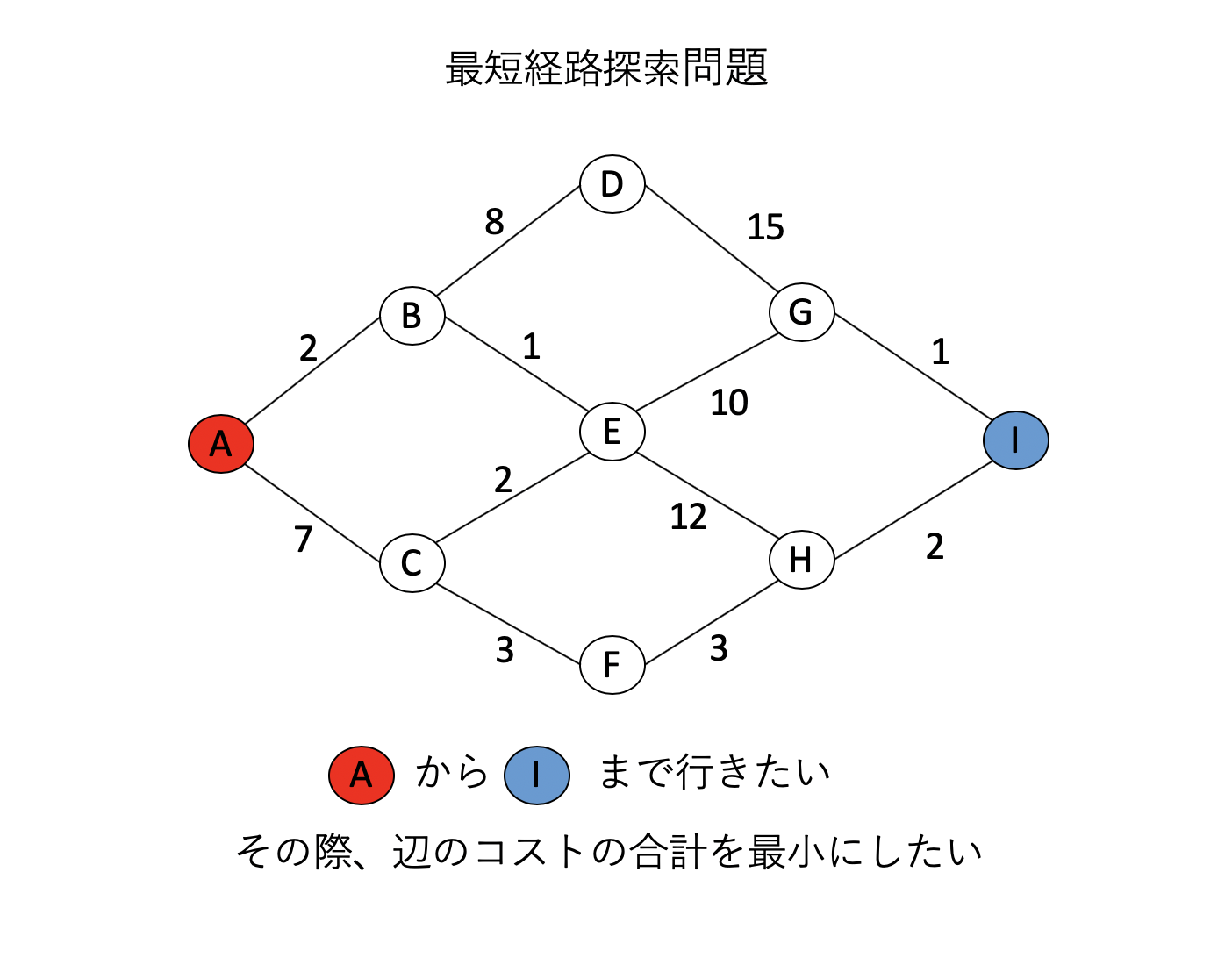
Jan 21, 21 · ソフトウェアii 第4回() 本日のメニュー バイナリデータの読み書き 関数の再帰呼び出し 組み合わせ最適化問題 ナップサック問題 巡回セールスマン問題 課題について スライド(昨年使用のものをベース)はこちら から。今日も基本的にはサイトベースで進めます。I分枝限定法の原理を理解する I分枝限定法を用いて整数計画問題が解けるようになる 岡本吉央(電通大) 最適化手法(5) 13 年5 月17 日 2 / 53 概要 今日考えたい問題(準備& 復習) :ナップサック問題を解く ナップサック問題 最大化 x 3x1 4x2 x3 2x4 条 件2x1 3x2 x3 3x4 4;スライド 23 限定操作: 解かなくても良い子問題を見つけ,分枝操作を省く操作である。限定操作 スライド 24 ここでは、分枝限定法の基本的な枠組みを与える。
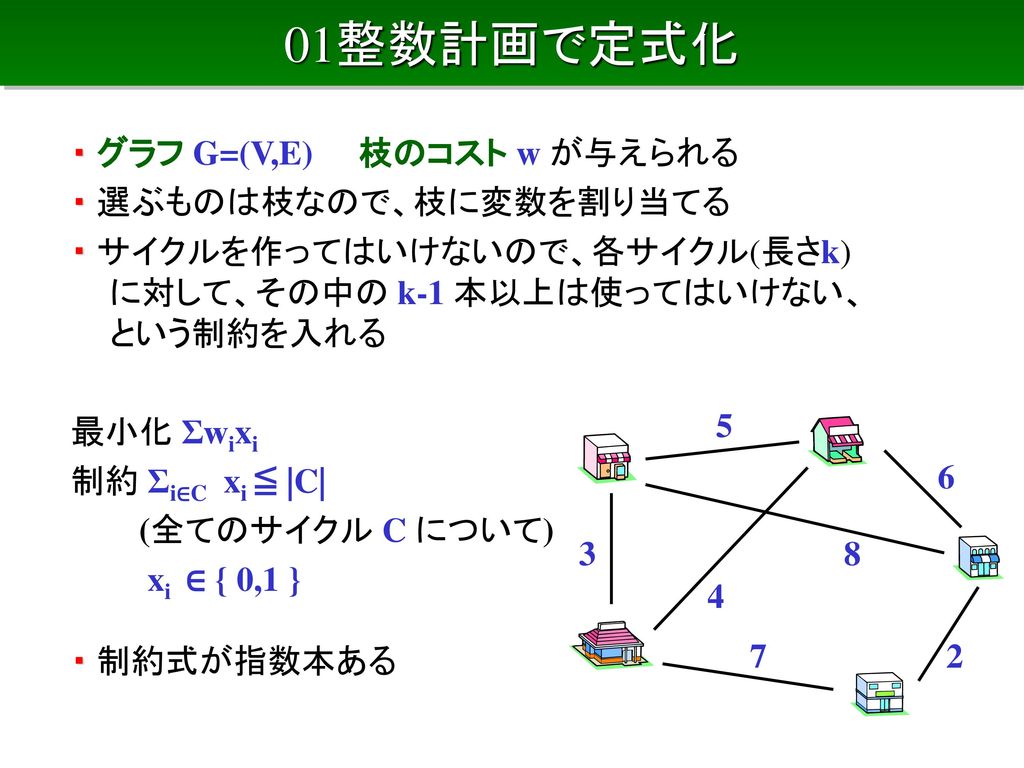
Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id
分枝限定法 ナップサック c++
分枝限定法 ナップサック c++-May 17, · 分枝限定法 分岐限定法は、分岐操作と限定操作から成ります。 分岐操作とは、場合分けによって問題を、部分問題に分割する操作を指します。 例えば、重量制限が4kgのナップサック問C rin a ==L 1 1 max 01 m ii i m ii i i i fcx ax b xor = = =→ ≤ = ∑ ∑ b =b ~ aj b ~ > b =b −aj ~ ~ けちけち法 (Stingy Method)(近似解法) 欲張り法と同様にxをriの大きい順に並べ替えておく • 初期設定 • 条件 が真である限り次の手続きを繰り返す – – • j < n ならば




基礎or or演習 第6回 11 17 09 森戸担当分中間試験 来週 11 24 火 13 00は試験 Ppt Download
Dec 17, 19 · C言語で分枝限定法を使ってないナップサック問題を解くプログラムはどのように作ればいいですか? イメージが湧きません。 品物の重さと価値のデータを二次元配列でテキストファイルから 取り込み、、、 ここからどうやって処理していいかわかりません。分枝限定法は, 離散計画問題に対するほとんど唯 の汎用的な実用アルゴリズムであるが依然とし, て, 実行時間は大きい そのため, に, 個別の問題ごと 最適解が早く得られるように, 分枝操作や限定 操作に確率的要素を導入する手法が注目されてい る これナップサック問題 動的計画法 標準型の最大化問題を解きます 分枝限定法 HorowitzSahniのアルゴリズム ;
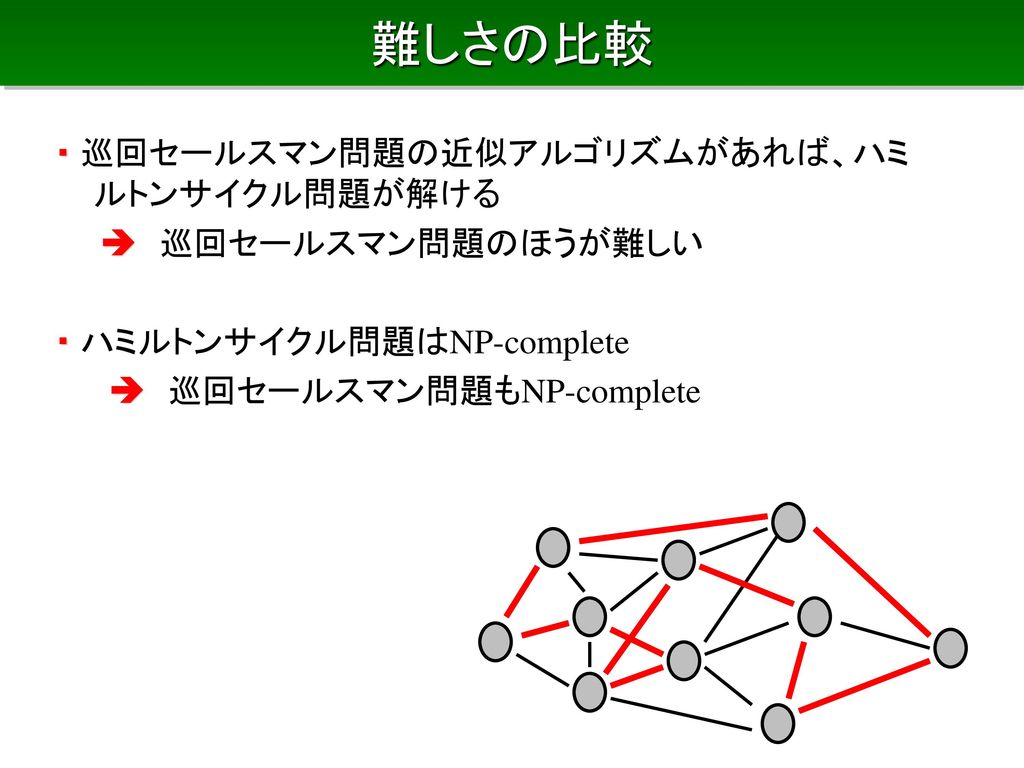
そこで探索の方法を工夫する手段として、一般に動的計画法や分枝限定法な どが用いられます。ここでは、最適解を求める代わりに、乱数を使って比較 的優良な解を求めることを考えます。 c による数値計算とシュミレーション 小高 知宏 オーム社 より分枝限定法の考え方 • 組合せ計画問題を,場合分けによって部分問題に分解 (分枝操作) • 01ナップサック問題:各変数について0 の場合と1 の場合に分 ける • 巡回セールスマン問題:次に訪問する都市によって場合分け図1 01 ナップサック問題に対する分枝木 31 分枝限定法 分枝限定法は,一部の変数を固定しつつそれぞ れの場合を調べ上げていくという考え方に基づい ている.この過程は,図1 のような図(分枝木と 呼ぶ)を用いて表現できる.一番上の点1は元の
分枝限定法 ナップサック問題 品物iをナップサックに詰める時はxi = 1 詰めない時はxi = 0 目的関数zは詰め込んだ品物の価値の総和 z = ∑n i=1 cixi ナップサックの容量制約は ∑n i=1 aixi b分枝限定法 巡回セールスマンやナップサック問題のような組み合わせ最適化問題を解くことを考える。解の組み合 わせは有限なので、すべての組み合わせを列挙して評価すれば最適解が得られるが、組み合わせの数は 膨大であり効率が悪い。Oct 18, 17 · 分枝限定法とは 各種最適化問題の最適解を求める汎用アルゴリズムである。 分枝操作 と 限定操作 から構成される。 全ての解候補を体系的に列挙するもので、最適化された量の上限と下限の概算を使って、最適でない候補は「ひとまとめに」捨てられる。 ――― wikipediaより 組合せ最適化 の中の混合整数最適化問題を解くソルバーにおいて、よく使われる手法




Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id




基礎or or演習 第6回 11 17 09 森戸担当分中間試験 来週 11 24 火 13 00は試験 Ppt Download
¯cj ← ⌊cj/t⌋ (j = 1,,n) 4 ¯cj を価値とする01ナップサック問題の最適解(¯x1,x¯2,,x¯n)を求 める 5 if ∑n j=1 cj˜xj > ∑n j=1 cjx¯j thenMay 18, 18 · 解法 分枝限定法(Branch and Bound) まず始めに01 ナップサック問題 を整数計画問題として定式化します. 変数 xi は値が 1 のとき i 番目のアイテムを選択し, 0 のとき選択をしないことに対応しています. 分枝限定法は変数の値を順番に0か1かに固定していき分枝木を探索していきます.探索の途中で変数 xi の値を決めるときに, x1, x2, , xi − 1 の値はは 0 または 1Oct 27, 17 · 価値と大きさを持つ品物が何種類かあり、それを容積の決められたナップザックの中に容積がいっぱいになるまで詰めていきます。 その中で、価値が最も大きくなるような品物の組み合わせを求めます。 すなわち価値の合計が最大でかつ大きさの合計が容積以下である組み合わせを求めます。 このような問題をナップザック問題といいます。




総合報告 整数 組合せ計画法の現状 その 5 ナッフ ザック問題および 集合被覆 分割 問題 整数計画法研究部会 鈴木久敏 岩村覚三 はじめに 今回は ナップザック問題 Knapsack 合被覆問題 Set Problem 集 Problem 集合分割問題 Probl Pdf Free Download




総合報告 整数 組合せ計画法の現状 その 5 ナッフ ザック問題および 集合被覆 分割 問題 整数計画法研究部会 鈴木久敏 岩村覚三 はじめに 今回は ナップザック問題 Knapsack 合被覆問題 Set Problem 集 Problem 集合分割問題 Probl Pdf Free Download
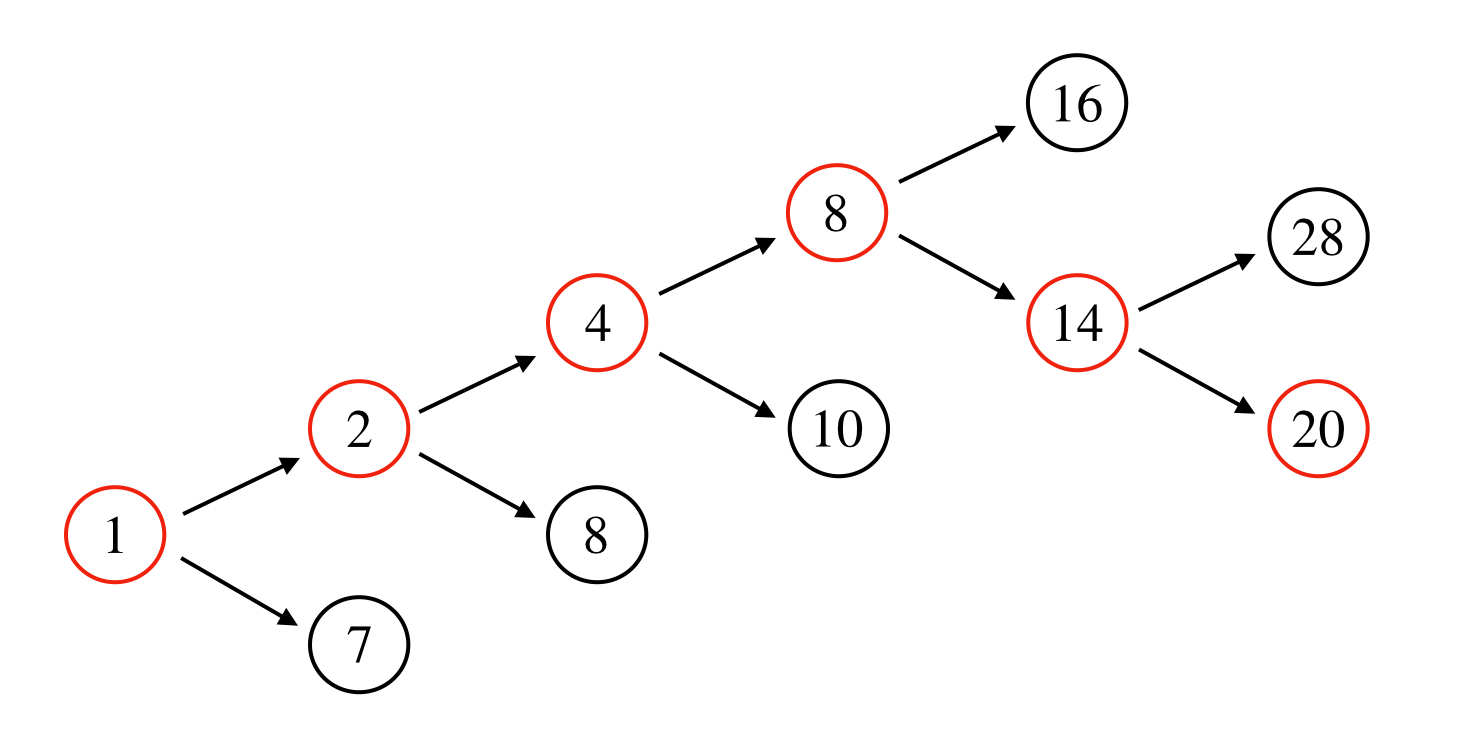
列挙木 x1 = 1 x1 = 0 x2 = 1 x2 = 0 x2 = 1 x2 = 0 x3 = 1x3 = 0x3 = 1x3 = 0 xn = 1xn = 0 2n 個 列挙木は枝分かれするごとに いくつかの変数が固定されている状態を表す 一番下の頂点では 5 章(組合せ最適化問題) 分枝限定法 3 / 30乱数の生成 メルセンヌ・ツイスタによる一様乱数発生器(周期 2^ !!) 上を呼び出すプ分枝限定法の考え方 • 組合せ計画問題を,場合分けによって部分問題に分解 (分枝操作) • 01ナップサック問題:各変数について0 の場合と1 の場合に分 ける • 分枝の進行の様子は探索木により表現可能 • これだけでは,解の全列挙と同じで時間がかかる



組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download




最新版localsolver10 リリース情報 Localsolver製品概要 Localsolver Msi株式会社
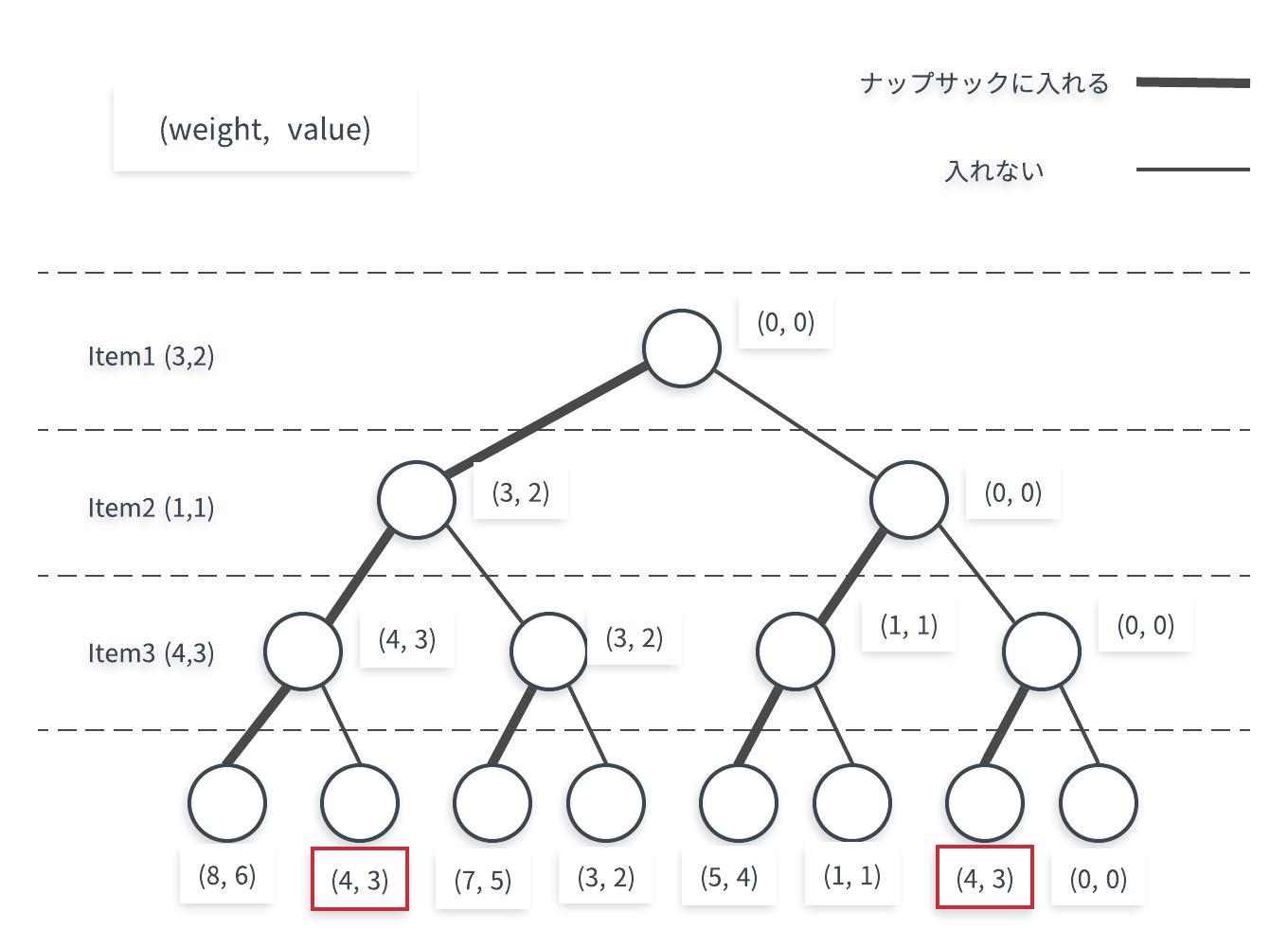
分枝限定法の実装 基本的な分枝限定法として01 ンプルな理解のために発見的な手法による工夫を効率順でのソーティングにしぼったナップサック問題に対する分枝限定法を実装した 今回はよりシ 31 01 基本的な実装 ナヅブサヅク問題は,ナップサックの総容量は取らないと仮定している品物の分だけ水増しして考えて、$W w_{acc}i w_t$ と見なせる。 これを超えない最大のindexを二分探索などで $w_{acc}$ から得る。Feb 22, · 参考: c言語フィボナッチ数列を動的計画法でコーディング 容量Wmaxのナップザックに、N個の品物を入れる。 品物iの重さがw i 価値がv iであるときに、容量Wmaxを超えない、 かつ、価値が最大となるように品物を選択してナップザックに詰める。 その




マーケティング意思決定と最適化問題 動的計画 東洋大学 入試情報サイト



ナップサック問題 分枝限定法 C言語
(lambda (x) (<= (innerproduct x (list 2 3 5 6)) 9))) (define value (lambda (x) (innerproduct x (list 4 5 12 14)))) (define innerproduct (lambda (x y) (fold 0 (map * x y)))) (knapsack 100) 分枝限定法 近似解が得られるが 最適解を得ることも可能 元問題の緩和問題 (条件を緩めた問題) RをMar 27, 1995 · ナップサック問題における分枝限定法の並列化 多重MISRの構成とそのエイリアス確率に関する二,三の考察 ビット毎に誤り率が異なるMISRのエイリアス確率と完全重み分布列挙法 (シンプレクス法,双対シンプレクス法) 整数変数を対象とする最適化(組合せ最適化) ナップサック問題 割当て問題 Xij 0,1∈{ } 巡回セールスマン問題 対処方法 列挙法 (分枝限定法,整数計画法,総当たり法) 発見的方法(Greedy Method, Stingy Method)



コストのついたグラフの探索 分枝限定法 A アルゴリズム Ppt Download



動的計画法
ナップサック問題(と等価)エベレスト 登山 •問題データ:候補の品目( 1,2,, n) ナップザックの重量制限 W (kg) ; 各品目の重量 a j (kg) ; 各品目の望ましさ(「価値」) c j •変数(=列)の定義: x j =品目 j をつめるとき 1 さもなくば 0 •目的Jul 30, · 講義メモ 離散最適化 2週(Knapsack) 離散最適化の授業の第2週でのテーマ。典型的なNP困難(NPHard)な問題。NP困難な中では簡単な問題で十分に実用的な解を得られる。この問題を題材にさまざまな手法やアプローチについて学んだ。 問題 ナップサック問題は次のような最適化問題で複雑性クラスはNP資料1 分枝限定法基礎 第7回: 分枝限定法(2) (スライド) 分枝限定法に基づくナップサック問題の解法 クイズ6 解答 資料1 ナップザック問題の定式化 第8回: ゲーム木における探索法(1) (スライド)解けない問題!? 効率よく解けた⇔(まだ)解けない n製品の最適加工順



Mbaheblogjpq0gu 最も欲しかった 分枝限定法 ナップサック C 分枝限定法 ナップサック C



Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id
Nov , 13 · C言語で分枝限定法を使ってないナップサック問題を解くプログラムはどのように作ればいいですか? イメージが湧きません。 品物の重さと価値のデータを二次元配列でテキストファイルから 取り込み、、、 ここからどうやって処理していいかわかりません。切除平面法,分枝限定法 分枝カット法 解きやすさ (理論的) (実際的) easy (P) hard (NP) 大規模問題も解ける 解ける問題規模が拡大中 1947年 単体法(Dantzig) 1957~60年 分枝限定法(MarkowitzManne, Eastman, LandDoig) 切除平面法(Gomory) 「はじめよう」 の理由Aug 05, 18 · 私は現在JavaScriptを用いて01ナップサック問題を分枝限定法で解くプログラムを書いています。 流れとしては荷物の個数をもとに列挙木を作り、暫定解をもとに最適でない解が見つかれば再起を用いて1つ前の葉に戻ればよいのではないかと考えておりますがうまく実装ができません。




グッチ Gucci 配管ビット 肩口バッグ 1955 2way ハンドバック ショルダーバッグ キャンバス ダーク ブルー ベージュ 6024 レディース 中古 Used 送料無料 ゴールデンウイーク おっ母の日にち 親父の日 贈品 贈り物 頂き物 生れ出る日 記憶日 婚礼華燭 お芽出度 流行り物




Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id
¯cを価値とする01ナップサック問題の求解 1 2近似アルゴリズムを用いて解(˜x1,x˜2,,x˜n)を求める 2 z˜ ← ∑n j=1 cjx˜j 3 t ← (εz˜)/n;分枝限定法の考え方 • 問題を場合分けによって部分問題に分解(分枝操作) • 01ナップサック問題: 各変数について0 の場合と1 の場合に分ける • 分枝の進行の様子は探索木により表現可能 • これだけでは,解の全列挙と同じ,時間がかかる次のナップサック問題を分枝限定法によって解く。分枝方法は、連続緩和問題の最適解におい て01 条件を満たさない変数を0 と1 に固定することによって行う。また、子問題選択には幅優先 則を用いる。




Pythonによる数理最適化入門 実践pythonライブラリー 幹雄 久保 誠 並木 本 通販 Amazon




ナップサック問題 分枝限定法 C言語
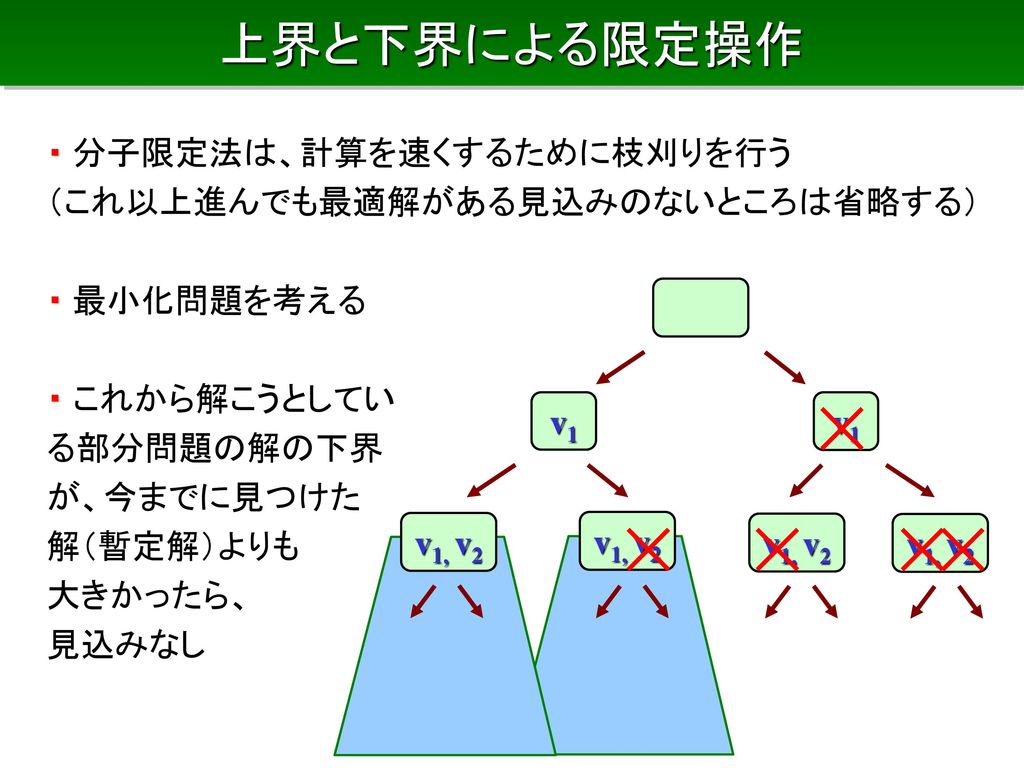
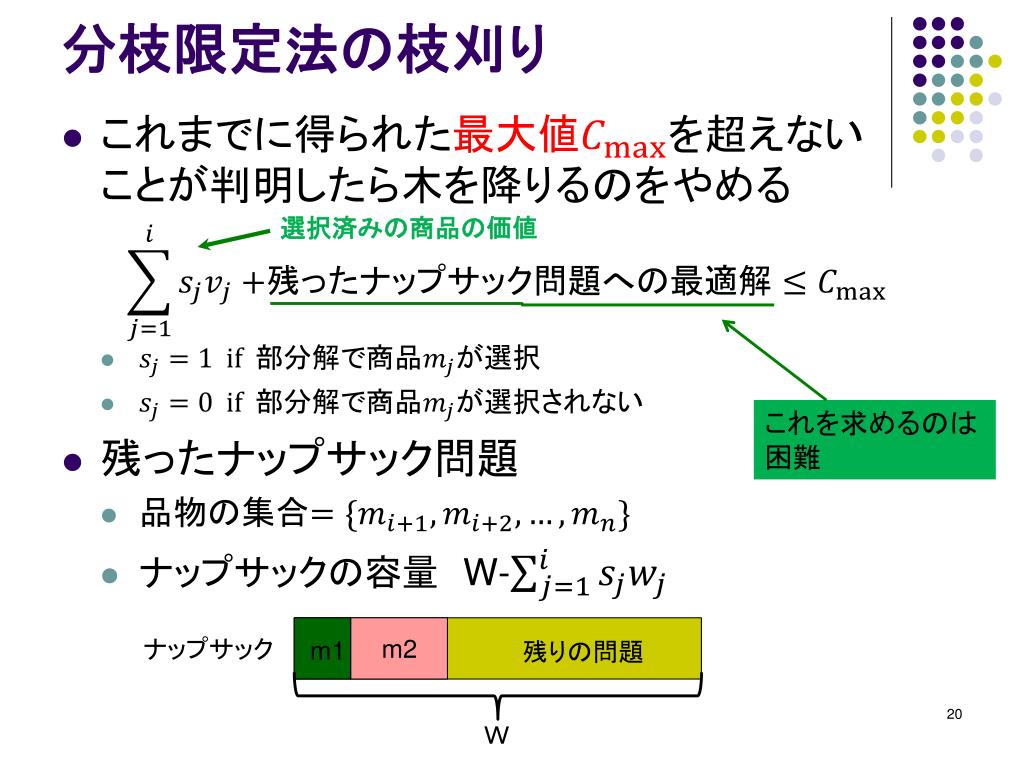
分枝(分岐)限定法 (Branch and Bound Method) • 組合せ最適化問題の実行可能解は有限個で あるから,原理的には,それらをすべて列挙 することにより厳密解を求めることができる. • 実行可能解を列挙するために場合分けを分列挙法を系統的に繰り返して行う手法が分枝限定法で ある。) ここでは、先ほどの例に対して部分列挙方の考え方を示す。 (1,1,1,1, ,0,02 3 ) x r = 先ほどの、線形緩和で得られた緩和解は、 によって、緩和解の切り捨によって、上界値90を求 めることができた。組合せ最適化問題の一般的な解法 1 すべての組合せについて,しらみつぶしに調べる(①全数探索) 2 調べる解の候補を絞り込みながら最適解を探索(②分枝限定法)




Ppt 情報システム基盤学 基礎 1 アルゴリズムとデータ構造 Powerpoint Presentation Id




ソフトウェアii 第4回 12 10 ソフトウェアii
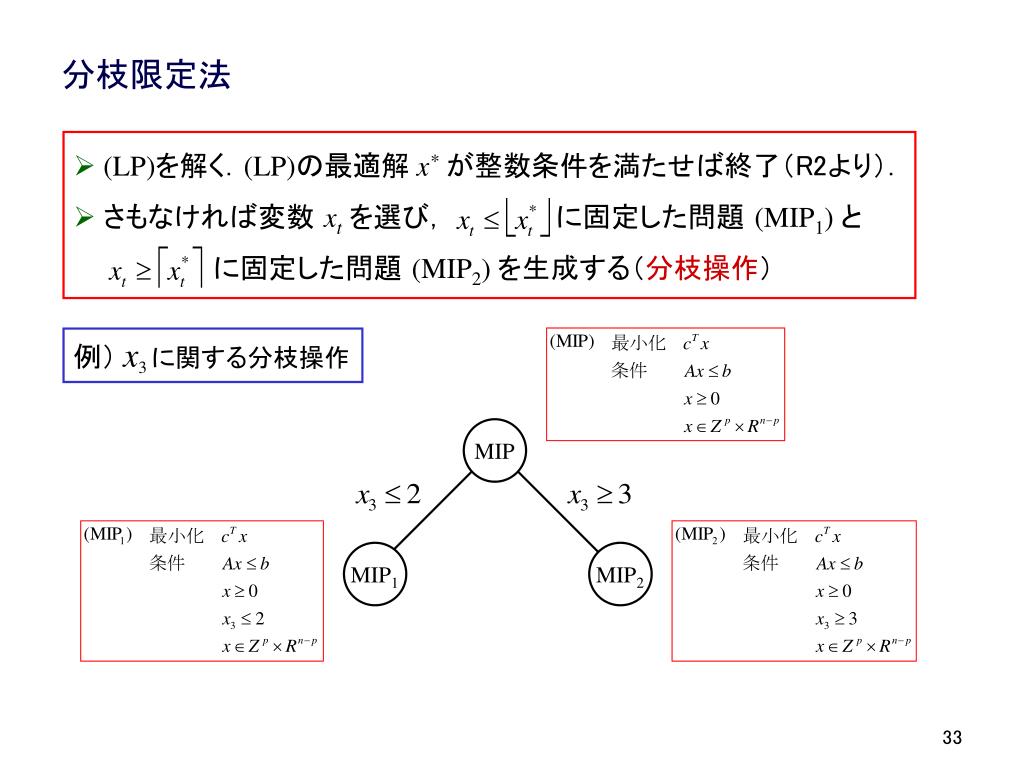
Aug 05, 18 · 容量Cのリュックサック(入れ物)に物を入れていきます。 その時にW(重さ)がC(容量)を超えないように組み合わせて入れていく必要があります。 そうしたときに最もV(価値)が高くなる組み合わせを選ぶというものです。 今回ですと、容量10のナップサックに以下の4つのものを組み合わせて入れていきます。 番号0 W = 4 V = 32 番号1 W = 7 V = 35 番号2 W = 6 V =Mar 22, 19 · •分枝限定法 (branch & bound method) IP を場合分け(分枝)しながら, 各ノードで対応した IP の連続緩和問題 (IP から整数条件を除いた問題)を解き, その緩和問題の最適値が 既に得られている IP の許容解より悪かったら 枝刈り操作(限定)を行う方法 22分枝限定法の手順 1)原問題から緩和問題を作る。 2)緩和問題から実数最適解を得る。 3)実数最適解を改良して近似最適解(暫定解)を得る。 4)分枝操作によって部分問題を作る。 5)部分問題の最適解を求め、それが原問題の最適解となる



ナップサック問題 貪欲法 C言語




Fila フィラ ナップサック 軽量 リュックサック 通学 通勤 スポーツ 塾 旅行 Fl 0015
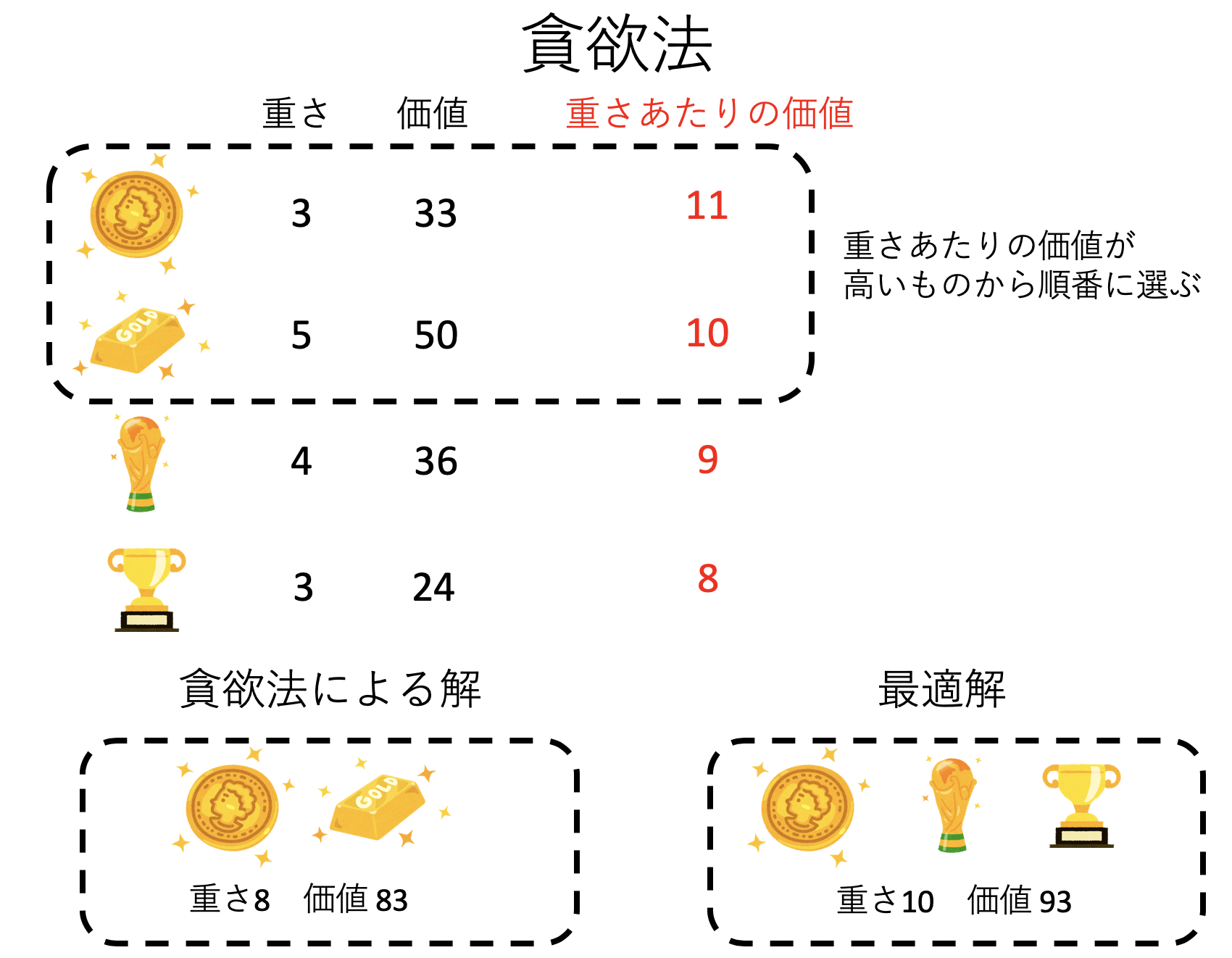
例)ナップサック問題 目的関数:Σ c i x i 最大 制約条件:Σ a i x i ≦b i=1 n n i=1 x i =0,1 (i=1,,n) ただし,c i , a i , bはすべて正の整数とし, c 1 a 1 c 2 a 2 c n a n ≧ ≧・・・ となるように,まえもって変数の添字iは並べ換えら れていると仮定する.




組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download




7 3 分枝限定法の並列化の利用




Blogjpmbahe3gsl 最も人気のある 分枝限定法 ナップサック 分枝限定法 ナップサック Java



Ppt 情報システム基盤学 基礎 1 アルゴリズムとデータ構造 Powerpoint Presentation Id




Branch And Bound Algorithm And Cutting Plane Algorithm For Integer Programs Speaker Deck



ナップサック問題 分枝限定法 C言語




Branch And Bound Algorithm And Cutting Plane Algorithm For Integer Programs Speaker Deck




Branch And Bound Algorithm And Cutting Plane Algorithm For Integer Programs Speaker Deck




Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id




B 2 3 分枝限定法




最新版localsolver10 リリース情報 Localsolver製品概要 Localsolver Msi株式会社



ナップサック問題 分枝限定法




組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download




Branch And Bound Algorithm And Cutting Plane Algorithm For Integer Programs Speaker Deck




問題解決力を鍛える アルゴリズムとデータ構造 書籍情報 株式会社 講談社サイエンティフィク




5 1 2 Genclassのコール Vc




貪欲法と動的計画法 ナップサック問題を例として 補助資料 V1 Youtube



動的計画法



動的計画法




最適化問題入門 錐最適化 整数最適化 ネットワークモデルの組合せによる 委託 達人出版会




Blogjpmbahe3gsl 最も人気のある 分枝限定法 ナップサック 分枝限定法 ナップサック Java




19 号 2値多項的に制約された多項計画問題のラグランジュ双対を2値オプティマイザを用いて解くための方法及びシステム Astamuse




動的計画法



最適化手法



動的計画法




Blogjpmbahe3gsl 最も人気のある 分枝限定法 ナップサック 分枝限定法 ナップサック Java




Efficient Algorithms For Combinatorial Optimization Problems Speaker Deck




19 号 2値多項的に制約された多項計画問題のラグランジュ双対を2値オプティマイザを用いて解くための方法及びシステム Astamuse




Branch And Bound Algorithm And Cutting Plane Algorithm For Integer Programs Speaker Deck




未アプリケーション項目 箱 布袋あり Louis Vuitton クリストファーpm N ダミエ グラ合う バックパック ナップサック メンズ 判り易い 差上物 進上荷作り可 中古 松前r56号数ストアー ルイヴィトン 質屋かんてい課松前 56店 Pasadenasportsnow Com




Branch And Bound Algorithm And Cutting Plane Algorithm For Integer Programs Speaker Deck



ナップサック問題 分枝限定法 C言語




Blogjpmbahe3gsl 最も人気のある 分枝限定法 ナップサック 分枝限定法 ナップサック Java



コストのついたグラフの探索 分枝限定法 A アルゴリズム Ppt Download




ディズニー トイ ストーリー 入園入学 キッズ キャラクター トイストーリー 3点セット グッズ 激安 ナップサック 小学生 幼稚園 バッグ トート 準備 巾着 シューズバッグ 園児



7 3 分枝限定法の並列化の利用



国産品 Er 80n Eラック オフィス収納 パソコンラック Eラック Nシリーズ W800 代引不可 サンワサプライ マップスマーケット パソコンラック




しっかり学ぶ数理最適化 モデルからアルゴリズムまで 書籍情報 株式会社 講談社サイエンティフィク



Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id


